Stats say Hot Hand is real | Klay Thompson’s amazing quarter
October 29, 2015 Leave a comment
Want to see something amazing? Take two minutes to watch what Golden State Warriors guard Klay Thompson did in the third quarter of a January 2015 game:
Klay is a great shooter in general, but that performance was unreal. He hit 13 shots in a row, 9 of which were three-pointers. It’s what I characterize as a “Hot Hand”. If you’ve played basketball, you likely understand the Hot Hand. Every shot feels like it’s going in, and it does. You can “feel” the definitive arc to the basket. There’s a hyper confidence in every shot. I like the way Jordan Ellenberg describes it on Deadspin:
The hot hand, after all, isn’t a general tendency for hits to follow hits and misses to follow misses. It’s an evanescent thing, a brief possession by a superior basketball being that inhabits a player’s body for a short glorious interval on the court, giving no warning of its arrival or departure.
The Hot Hand arrives when it damn well chooses, and leaves the same way. Clearly, it had an extended stay with Klay Thompson that night.
But, there is research that dismisses the notion of the Hot Hand. In 1985 Cornell and Stanford researchers – Thomas Gilovich, Robert Vallone, Amos Tversky – conducted an analysis (pdf) of their definition of the Hot Hand. Here’s how they describe a Hot Hand:
First, these terms imply that the probability of a hit should be greater following a hit than following a miss. Second, they imply that the number of streaks of successive hits or misses should exceed the number produced by a chance process with a constant hit rate [i.e. field goal percentage].
They also polled fans, and got these responses:
The fans were asked to consider a hypothetical player who shoots 50% from the field. Their average estimate of his field goal percentage was 61% “after having just made a shot,” and 42% “after having just missed a shot.” Moreover, the former estimate was greater than or equal to the latter for every respondent.
Their research, some of which is replicated below for analyzing Klay Thompson, showed that the belief in the Hot Hand is misguided. The streaks of made shots by players are all part of the normal distribution of shots one would expect statistically.
Oh, but that Klay Thompson quarter…! Let’s look at Klay Thompson’s performance to see if he really did have a Hot Hand.
Klay’s shooting history
To analyze Klay’s performance, we need data. Fortunately, the NBA provide handy stats on its players. I was able to get two seasons (2013-14, 2014-15) of shooting data for Thompson. The data includes the game, shot sequence, shot distance and whether the shot was made or not.
Klay is a 45.4% shooter from 2013-2015, taking 2,514 shots in 157 regular season games. I wanted to get a sense of how he shoots from different ranges, so I categorized his shots in four buckets:
- Short: < 9 ft
- Midshort: 9 – 16 ft
- Midlong: 16 – 23.7
- Long: >= 23.7 ft
With the ranges, we gain some insights about how Klay operates:
You can see in the left chart that he prefers longer shots. However, his shooting percentage is significantly better for close-in shots. Because of the marked difference between his short range shooting (55.7%) and the other distances, I’m going to remove shots taken from less than 9 feet away. Making close-range shots (e.g. layups) is not an example of a Hot Hand; that designation is reserved for longer shots.
Geeking out
You can see the data files on Github: 2013-14, 2014-15. They were combined to do the analysis. This R function categorizes the shots according to their distance.
Comparing Klay against the researchers’ definition of Hot Hand
Let’s look at a couple aspects of Klay’s performance vis-a-vis the analytical framework of the Cornell and Stanford researchers.
First, they looked at what happens after a player makes a shot. Did they have a higher shooting percentage after a made shot? In a modified version of this test, I looked at the set of longer shots that were taken consecutively. If there was a tendency to shoot higher percentages after a made shot, there must be a corollary lower shooting percentage after missed shots.
This table shows the longer shot FG% in aggregate for Klay Thompson after (i) made longer shots; (ii) missed longer shots; and (iii) when he hasn’t taken a prior longer shot. That third (iii) scenario includes both the first shot of a game, and cases where he shot a short ( < 9 ft) basket prior to taking a longer shot.
| Scenario | FG% |
| When Klay makes a shot, the FG% on his next shot is… | 43.2% |
| When Klay misses a shot, the FG% on his next shot is… | 42.5% |
| When Klay hasn’t taken a prior longer shot, the FG% on his shot is… | 41.3% |
| His overall FG% for longer shots (>= 9 feet) is… | 42.4% |
Looking at the table, what do you notice? His highest field goal percentage occurs after a made shot! Does that validate the belief that shooters “get hot” after making a shot? Unfortunately, no. Statistical analysis dismisses that possibility; which if we’re honest with ourselves, is the right call. There’s not enough of a difference in FG% after a made shot. This is consistent with the Cornell and Stanford researchers’ findings.
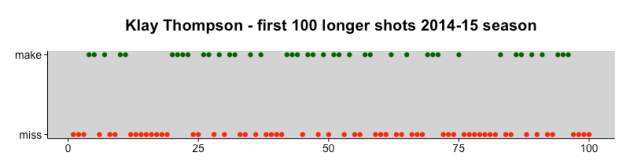
Next, there’s the question of whether Klay’s individual shots show any kind of pattern that’s not random. As an example, look at the graph of makes and misses for his first 100 longer (>= 9 ft) shots of the 2014-15 season:
You can see there are a number of runs in there. For instance, shots 12 – 19 are all misses, followed by shots 20 – 23, which are all makes. Maybe Klay’s shooting does exhibit a pattern misses-follow-misses, and makes-follow-makes? Turns out…no. Statistical analysis shows that the patterns of makes and misses are entirely random. This is consistent with the findings of the Cornell and Stanford researchers.
Finally, we look at an analysis that the researchers did on some NBA players back in 1985. They broke up the players’ shooting histories into sets of four shots. They then looked at each set of four shots. They wanted to see if there were higher frequencies of 3 or 4 made shots per set, as well as higher frequencies of 0 and 1 missed shot per set, than one would expect to happen normally. If so, that would indicate “streakiness” (i.e. evidence of Hot Hand).
I’ve run that analysis for Klay’s two seasons below:
| 0 made | 1 made | 2 made | 3 made | 4 made | |
| Actual | 55 | 152 | 184 | 77 | 18 |
| Expected | 54 | 158 | 174 | 85 | 16 |
As you see, Klay’s actual “made” frequencies are close to what would have been expected. Statistical analysis confirms: there is no unexpected streakiness in his shooting. This is consistent with the findings of the Cornell and Stanford researchers.
At this point, maybe the researchers were right! Klay hasn’t shown any evidence of a Hot Hand.
Geeking out
Prior shot analysis: For the prior shot analysis, I looked at only longer shots (i.e. >= 9 ft). But I also wanted them to be actual prior-next pairs of shots. That means I didn’t want the analyze the impact of a prior short shot on a subsequent longer shot. To keep the data set focused only on consecutive longer shots, I wrote this R program.
Both the prior shot and the next shot were coded as 0 (miss) and made (1). These values were aggregated into a 2×2 table:
| next miss (0) | next make (1) | |
| prior miss (0) | 436 | 366 |
| prior make (1) | 322 | 278 |
A Fisher’s exact test was then run on the table. The p-value is 0.8285. The null hypothesis that the next misses and makes are not correlated to prior misses and makes is accepted.
Runs of makes and misses: The entire sequence of 1,945 longer shots over two seasons were subjected to a test of randomness. I held off breaking the sequences into individual games, believing that such extra work would not yield materially different results. The specific test of randomness was the Bartels Ratio Test (background here) in R. The null hypothesis of randomness is accepted with a p-value of 0.9935.
Sets of four shots: For the actual number of made shots per set, first I broke the two seasons of Klay’s shots into 486 groups of four, via this R program. I then aggregated these into a table. For the expected number of made shots for 486 simulated groups of four, I created a binomial tree. The tree took Klay’s longer shot FG% for its probabilities: make @ 42.365%, miss @ 57.635%.
The actual numbers of made shots per set (i.e. 0 – 4) were compared to the expected number with simple correlation. The correlation coefficient is .99, with a p-value of 0.0005. The null hypothesis that the numbers aren’t covariant is rejected. Which in this case, means Klay’s sets of four didn’t show any unexpected variances (i.e. concentrations of makes and misses).
Evidence for Klay’s Hot Hand
OK, I’ve managed to show that Klay Thompson’s performance matches the results found by researchers Gilovich, Vallone and Tversky. But we saw what he did in that third quarter. Excluding the two short shots from that third quarter, Klay made 11 shots in a row. He was shooting out of his mind. What says that was evidence of a Hot Hand?
We can start by assessing the probability of hitting 11 longer shots in a row. As an example of how to do this, consider the coin flip. 50/50 odds of heads or tails. What are the odds of getting 3 heads in a row? You multiply the .5 probability three times: 12.5% probability of three heads in a row.
Klay’s FG% for longer shots is 42.4%. Let’s see what the probability of 11 made shots in a row is:
0.424 ^ 11 = 0.00789%.
Whoa! Talk about small odds. Over the course of Klay’s two seasons, he had roughly 177 sets of 11 shots. The expected number of times he’d make all 11 shots in a set is: 0.00789% of 177 = 0.013 times. Or looked at another way, we’d expect 1 such streak for every 12,674 sets of 11 shots, or 140,404 shots! Klay would need to play 144 years to shoot that many times.
Next, let’s look at the streaks Klay actually had over the two seasons:
The most common streak (292 of them) is 1 basket, which may violate your sense of a “streak”. But it’s important to measure all the intervals of streaks, including those with only 1 basket.
At the other end of the spectrum, look at that 11-shot streak. It really stands out for a couple reasons:
- There’s only one of them. It’s very rare to hit 11 longer shots in a row.
- There’s a yawning gap from the next longest streak, 7 shots. There was only 1 seven-shot streak as well.
When Klay starts a new streak (i.e. hits an initial longer basket), his average streak is 1.68 made shots in a row. I ran a separate statistical analysis from the 11 “coin flips” example above. Using his average of 1.68 streaks, the odds that he would hit 11 in a row are 0.0000226%. This ridiculously low probability complements the “coin flips” probability described above of 0.00789%.
Using either number, the point is this:
Klay’s streak of 11 made shots is statistically not supposed to happen. The fact that he had an 11-shot streak cannot be explained by normal chance. Something else was at work. This is the Hot Hand.
It is true that Hot Hands are rarer than fans think. Much of Klay’s shooting history validates the findings of the Cornell and Stanford researchers. But it is undeniable that Klay did have a Hot Hand in the third quarter of the January 2015 game.
I’m @bhc3 on Twitter.
Geeking out
To determine the number of streaks, I wrote an R program. The program looks at streaks only within games. There’s no credit for streaks that span from the end of one game to the start of the next game.
On a regular X-Y graph, the distribution of streaks is strongly right-skewed. Rather than use normal distribution analysis, I assumed a Poisson distribution. Poisson is most commonly used for analyzing events-per-unit-of-time; the unit of time is the interval. However, Poisson can be applied beyond time-based intervals. I treated each streak as its own interval. I then used the average number of shots per streak – 1.68 – as my lambda value. To get the probability of 11 shots in a streak, I ran this function in R: ppois(11, lambda = 1.68, lower = FALSE).


The Conversation